Yapay Sinir Ağları (YSA)

• Aynı zamanda derin sinir ağı olarak da adlandırılır.
• Sinir Ağı nedir: Temelde lojistik regresyon alıp en az 2 kez tekrar etmektir.
• Lojistik regresyonda girdi ve çıktı katmanları vardır. Ancak yapay sinir ağlarında giriş ve çıkış katmanı arasında en az bir tane gizli katman bulunur.
• Derin nedir, 'derin' demek için kaç katmana sahip olmam gerekir: 'Derin' göreceli bir kavram tabi ki bir ağın 'derinliği' anlamına geliyor yani kaç tane gizli katmanı olduğunu belirtiyor. Örneğin; 'Yüzme havuzunuzun derinliği ne kadar? ' 12 fit veya 2 fit olabilir, yine de bir derinliği vardır - yani 'derinlik' niteliğine sahiptir.
• NOT: Derin = Birçok gizli katman
• Neden gizli denir: Çünkü gizli katman girdileri görmez (eğitim seti)
• Örneğin bir girdi, bir gizli ve bir çıktı katmanınız var. Birisi size 'hey arkadaşım sinir ağınızın kaç katmanı var?' Cevap '2 katmanlı sinir ağım var' dır. Çünkü katman sayısı hesaplanırken giriş katmanı göz ardı edilir.
• 2 katmanlı sinir ağını görelim:
• Adım adım bu görseli öğreneceğiz.
  • Görüldüğü gibi girdi ve çıktı katmanları arasında bir gizli katman bulunmaktadır. Ve bu gizli katmanda 3 adet düğüm bulunmaktadır. Neden 3 düğüm seçtiğimi merak ediyorsanız, cevabı hiçbir sebep yok, sadece seçiyorum :). Düğüm sayısı, bir hiperparametredir. Bu nedenle yapay sinir ağının sonunda hiperparametreleri göreceğiz.
  • Giriş ve çıkış katmanları değişmez. Lojistik regresyon ile aynıdırlar.
  • Görselde sizin bilmediğiniz bir tanh fonksiyonu bulunmaktadır. Sigmoid fonksiyonu gibi bir aktivasyon fonksiyonudur. Tanh aktivasyon fonksiyonu, gizli katmanlar için sigmoid'den daha iyidir, çünkü çıkışının ortalaması sıfıra yakındır, bu nedenle verileri bir sonraki katman için daha iyi merkezler. Ayrıca tanh aktivasyon fonksiyonu, modelimizin daha iyi öğrenmesine neden olan doğrusal olmayanlığı arttırır.
  • Mor renk ile gördüğünüz gibi iki parçadır. Her iki kısım da lojistik regresyon gibidir. Tek fark aktivasyon fonksiyonu, girişler ve çıkışlardır.
    • Lojistik regresyonda: girdi = çıktı
    • 2 katmanlı sinir ağında: girdi = gizli katman = çıktı. Gizli katmanın 1. bölümünün çıktısı, 2. bölümün girdisi olduğunu düşünebilirsiniz.
• Bu kadar.
• 2 katmanlı sinir ağı için adımlar:

2-Layer Sinir Ağı

• Katmanların boyutu, başlangıç parametreleri ağırlıkları ve bias değeri
• İleri yayılma
• Loss function and Cost function
• Gradyan İniş ile Optimizasyon Algoritması
• Geri yayılma
• Parametrelerin güncellenmesi
• Öğrenilmiş ağırlık ve bias parametreleri ile tahmin
• Modelin oluşturulması

Katmanların boyutu ve başlangıç parametreleri ağırlıkları ve bias değeri

• Bildiğiniz gibi girdi, 4096 piksele sahip görüntülerimizdir (x_train'deki her görüntü).

• Her pikselin kendi ağırlığı vardır.

• İlk adım, her pikseli kendi ağırlıklarıyla çarpmaktır.

• Soru şu ki, ağırlıkların başlangıç değeri nedir?

  • Yapay sinir ağlarında anlatacağım bazı teknikler var ama bu sefer başlangıç ağırlıkları 0.01 alalım.
  • Tamam, ağırlıklar 0.01 ama ağırlık dizisi şekli nedir? Lojistik regresyonun hesaplama grafiğinden anladığınız gibi (4096,1)
  • Ayrıca ilk bias değeri 0'dır.

• 348 örneği olan x_train için $x^{(348)}$: $$z^{[1] (348)} = W^{[1]} x^{(348)} + b^{[1] (348)}$$ $$a^{[1] (348)} = \tanh(z^{[1] (348)})$$ $$z^{[2] (348)} = W^{[2]} a^{[1] (348)} + b^{[2] (348)}$$ $$\hat{y}^{(348)} = a^{[2] (348)} = \sigma(z^{ [2] (348)})$$

• Ağırlıkları rastgele başlatıyoruz. Çünkü parametreleri sıfırlarsak, ilk gizli katmandaki her bir nöron aynı hesaplamayı yapacaktır. Bu nedenle, gradyan inişinin çoklu yinelemesinden sonra bile, katmandaki her bir nöron, diğer nöronlarla aynı şeyleri hesaplayacaktır. Bu nedenle rastgele başlatıyoruz. Ayrıca başlangıç ​​ağırlıkları da küçük olacaktır. Başlangıçta çok büyüklerse, bu, tanh girdilerinin çok büyük olmasına ve dolayısıyla gradyanların sıfıra yakın olmasına neden olur. Optimizasyon algoritması yavaş olacaktır.

• Bias başlangıçta sıfır olabilir.

• Biraz kod yazalım..

# intialize parameters and layer sizes
def initialize_parameters_and_layer_sizes_NN(x_train, y_train):
    parameters = {"weight1": np.random.randn(3,x_train.shape[0]) * 0.1,
                  "bias1": np.zeros((3,1)),
                  "weight2": np.random.randn(y_train.shape[0],3) * 0.1,
                  "bias2": np.zeros((y_train.shape[0],1))}
    return parameters

İleri yayılma

• Piksellerden cost fonksiyona kadar olan tüm adımlara ileri yayılım denir.
  • z = (w.T)x + b => bu denklemde piksel dizisi olan x'i biliyoruz, w (ağırlıklar) ve b'yi (bias) biliyoruz, bu yüzden gerisi hesaplama. (T devriktir)
  • Önce z1'i gizli katmana göndeririz ve sonucu tanh fonksiyonundan geçiririz. Bu tanh fonksiyonu numpy kütüphanesinde mevcuttur. Daha sonra gizli katman çıkışındaki değerlerimizi o kısımdaki ağırlıklarla çarpıp bias değerlerini ekledikten sonra y_head (olasılık) döndüren sigmoid işlevine koyarız. Aklınız karıştığında gidin ve hesaplama grafiğine bakın. Ayrıca tanh ve sigmoid fonksiyonunun denklemi hesaplama grafiğindedir.
  • Sonra kayıp (hata) fonksiyonunu hesaplıyoruz.
  • Cost function tüm kayıpların (hata) toplamıdır.
  • z ile başlayalım ve z'yi giriş parametresi olarak alan ve y_head (olasılık) döndüren sigmoid tanımını(yöntemini) yazalım.

# calculation of z
#z = np.dot(w.T,x_train)+b
def sigmoid(z):
    y_head = 1/(1+np.exp(-z))
    return y_head
#y_head = sigmoid(z)

• Sigmoid yöntemini yazıp y_head'i hesapladığımız gibi. Lost (error) fonksiyonunun ne olduğunu öğrenelim
• Örnek yapalım, bir görüntüyü girdi olarak koydum, sonra ağırlıklarıyla çarpıyorum ve bias değerini ekleyerek z'yi buluyorum. Sonra z'yi tanh fonksiyonuna tabi tutun. Sonra z'yi sigmoid yöntemine koyun, böylece y_head'i bulurum. Bu noktaya kadar ne yaptığımızı biliyoruz. Sonra örneğin y_head, 0,5'ten büyük olan 0,9 oldu, bu nedenle tahminimiz bir işaretli bir görüntüdür. Tamam, her şey yolunda görünüyor. Ancak tahminimiz doğru mu ve doğru olup olmadığını nasıl kontrol edeceğiz? Yanıt, kayıp(hata) işlevindedir:

  * Log loss(hata) fonksiyonunun matematiksel ifadesi şu şekildedir: 
  

  * Yanlış tahmin yaparsanız kayıp (hata) büyük olur diyor.
      * Örnek: gerçek görüntümüz "bir" işareti ve etiketi 1 (y = 1), sonra y_head = 1 tahmini yapıyoruz. y ve y_head'i kayıp (hata) denklemine koyduğumuzda sonuç 0 oluyor. kayıp 0'dır. Ancak y_head = 0 gibi yanlış tahmin yaparsak kayıp (hata) sonsuzdur.
• Bundan sonra, cost fonksiyonu, kayıp fonksiyonunun toplamıdır. Her görüntü kayıp fonksiyonu oluşturur. Cost fonksiyonu, her girdi görüntüsü tarafından oluşturulan kayıp fonksiyonlarının toplamıdır.
• İleri yayılımı uygulayalım.

def forward_propagation_NN(x_train, parameters):

    Z1 = np.dot(parameters["weight1"],x_train) + parameters["bias1"]
    A1 = np.tanh(Z1)
    Z2 = np.dot(parameters["weight2"],A1) + parameters["bias2"]
    A2 = sigmoid(Z2)

    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

Loss function and Cost function

• loss ve cost fonksiyonları şu şekildedir: $$J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large\left(\small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large \right) \small $$

# Compute cost
def compute_cost_NN(A2, Y, parameters):
    logprobs = np.multiply(np.log(A2),Y)
    cost = -np.sum(logprobs)/Y.shape[1]
    return cost

Gradyan İniş ile Optimizasyon Algoritması

• Artık hata cost değerinin ne olduğunu biliyoruz.

• Bu nedenle cost değerini düşürmemiz gerekiyor çünkü biliyoruz ki cost değerinin yüksek olması yanlış tahminde bulunduğumuz anlamına geliyor.

• İlk adımı düşünelim, her şey başlangıç ağırlıkları ve bias ile başlar. Bu nedenle cost değeri onlara bağlıdır.

• Cost değerini düşürmek için ağırlıkları ve biası güncellememiz gerekiyor.

• Başka bir deyişle, modelimizin cost fonksiyonunu en aza indiren ağırlıkları ve bias değerini öğrenmesi gerekiyor. Bu tekniğe gradyan iniş denir.

• Bir örnek yapalım:

  * w = 5 ve bias = 0 değerlerine sahibiz (şimdilik bias yok sayın). Sonra ileri yayılım yaparız ve cost fonksiyonumuz 1.5'tur.
  * Buradaki gibi görünüyor. (kırmızı hat)

  

  * Grafikten de görebileceğiniz gibi, cost fonksiyonunun minimum noktasında değiliz. Bu nedenle minimum cost üzerinden gitmemiz gerekiyor. Tamam, ağırlığı güncelleyelim. ( := simgesi güncelleniyor anlamında)
  * w := w - adım. Soru şu ki, bu adım nedir? Adım slope1'dir. Tamam, olağanüstü görünüyor. Minimum noktayı bulmak için slope1'i kullanabiliriz. O zaman slope1 = 3 diyelim ve ağırlığımızı güncelleyelim. w := w - slope1 => w = 2.
  * Şimdi w ağırlığımız 2'dir. Hatırlayacağınız gibi yine ileri yayılımlı cost fonksiyonunu bulmamız gerekiyor.
  * w = 2 ile ileri yayılıma göre cost fonksiyonu 0,4 diyelim. Hmm, doğru yoldayız çünkü cost fonksiyonumuz azalıyor. cost fonksiyonu için cost = 0,4 olan yeni bir değerimiz var. Bu yeterli mi? Aslında bir adım daha deneyelim mi bilmiyorum.
  * Slope2 = 0.7 ve w = 2. ağırlığı güncelleyelim w : = w - step(slope2) => w = 1.3 bu yeni ağırlık. Yeni cost değerini bulalım.
  * w = 1.3 ve cost = 0.3 ile bir ileri yayılım daha yapın. Tamam cost değerimiz bile düştü iyi gibi ama yeterli mi yoksa bir adım daha mı atmamız gerekiyor? Cevap yine bilmiyorum, deneyelim.
  * Slope3 = 0.01 and w = 1.3. Güncellenmiş ağırlık w := w - step(slope3) => w = 1.29 ~ 1.3. Yani minimum cost noktası fonksiyonunu bulduğumuz için ağırlık değişmez.
  * Her şey güzel görünüyor ama eğimi nasıl bulacağız? Liseden veya üniversiteden hatırlarsanız, fonksiyonun eğimini (cost fonksiyonu) verilen noktadaki (verilen ağırlıkta) bulmak için, fonksiyonun verilen noktadaki türevini alırız. Ayrıca tamam peki eğimi buluyoruz ama nereye gittiğini nasıl biliyor diye sorabilirsiniz. Minimum noktaya gitmek yerine daha yüksek cost değerlerine çıkabileceğini söyleyebilirsiniz. Cevap, eğimin (türevin) hem adımı hem de adımın yönünü verdiğidir. Bu yüzden endişelenme :)
  * Güncelleme denklemi şudur. Bir cost fonksiyonu olduğunu söylüyor (ağırlık ve bias alıyor). Ağırlık ve bias'a göre cost fonksiyonunun türevini alın. Ardından bunu α öğrenme oranıyla çarpın. Ardından ağırlığı güncelleyin. (Açıklamak için bias görmezden geliyorum ancak bu adımların tümü bias için uygulanacaktır)

  

  * Şimdi eminim hiç bahsetmediğim öğrenme oranı nedir diye soruyorsunuz. Öğrenme oranını belirleyen çok basit bir terimdir. Ancak hızlı öğrenmekle hiç öğrenmemek arasında bir denge vardır. Örneğin, Paris'tesiniz (cari cost) ve Madrid'e gitmek istiyorsunuz (minimum cost). Hızınız (öğrenme oranınız) küçükse, Madrid'e çok yavaş gidebilirsiniz ve çok uzun zaman alır. Öte yandan, hızınız (öğrenme oranınız) yüksekse, çok hızlı gidebilirsiniz ama belki kaza yaparsınız ve Madrid'e hiç gidemezsiniz. Bu nedenle, hızımızı (öğrenme hızımızı) akıllıca seçmeliyiz.
  * Öğrenme oranı (learning rate), seçilmesi ve ayarlanması gereken hiperparametre olarak da adlandırılır. Diğer hiperparametreler ile L katmanlı yapay sinir ağlarında daha detaylı anlatacağım. Şimdilik, önceki örneğimiz için öğrenme oranının 1 olduğunu söyleyim.

• Sanırım artık ileri yayılımın (ağırlıklardan ve bias'dan cost değerine) ve geriye yayılımın (cost değerinden ağırlıklara ve bias değerlerini güncellemeye) arkasındaki mantığı anlıyorsunuz. Ayrıca gradyan inişini de öğrendiniz. Kodu uygulamadan önce bir şey daha öğrenmeniz gerekiyor, bu da cost fonksiyonunun ağırlıklara ve bias'a göre türevini nasıl aldığımızdır. Python veya kodlama ile ilgili değildir. Saf matematiktir. İki seçenek var birincisi google'da log-loss fonksiyonunun türevi nasıl alınır, ikincisi log-loss fonksiyonunun türevinin ne olduğunu google'da aramak :) Konuşmadan matematiği anlatamayacağım için ikinciyi seçiyorum :) $$ \frac{\partial J}{\partial w} = \frac{1}{m}x( yhead - y)^T$$ $$ \frac{\partial J}{\partial b} = \frac{1}{m} \sum{i=1}^m (y_head-y)$$

• Bu, derin öğrenmede makinelerin “öğrenmesidir” ……

• Umarım hayal kırıklığına uğramazsın :)

Geri yayılma (Backward Propagation)

• Geriye yayılım türev anlamına gelmektedir.
• Geri yayılım: Sinir ağında 𝜕𝐿∕𝜕𝑤’yı hesaplamanın etkili bir yoludur.
• Geri yayılım algoritması, sinir ağlarının eğitimi için çok önemlidir.
• Bir sinirsel ağdaki ağırlık değerlerinin, önceki elde edilen hata oranına dayanarak tekrar güncellenmesi işlemidir.
• Geri yayılım, ağırlıkları uygun şekilde ayarlayarak daha düşük hata oranlarının elde edilmesini sağlar ve modeli, genellemesini artırarak güvenilir kılar.
• Bu işlem, dört aşamadan meydana gelmektedir. Bunlar ileri gidiş, hata hesaplama, geri gidiş ve ağırlık güncelleme işlemleridir.
• Ancak mantık aynı, kod yazalım.

# Backward Propagation
def backward_propagation_NN(parameters, cache, X, Y):

    dZ2 = cache["A2"]-Y
    dW2 = np.dot(dZ2,cache["A1"].T)/X.shape[1]
    db2 = np.sum(dZ2,axis =1,keepdims=True)/X.shape[1]
    dZ1 = np.dot(parameters["weight2"].T,dZ2)*(1 - np.power(cache["A1"], 2))
    dW1 = np.dot(dZ1,X.T)/X.shape[1]
    db1 = np.sum(dZ1,axis =1,keepdims=True)/X.shape[1]
    grads = {"dweight1": dW1,
             "dbias1": db1,
             "dweight2": dW2,
             "dbias2": db2}
    
    return grads

Parametrelerin güncellenmesi

• Bu noktaya kadar öğreniyoruz
  • Başlangıç parametreleri (uygulandı)
  • İleri yayılım ve cost fonksiyonu ile cost değerini bulma (uygulandı)
  • Güncelleme (öğrenme) parametreleri (ağırlık ve bias). Şimdi uygulayalım.

# update parameters
def update_parameters_NN(parameters, grads, learning_rate = 0.01):
    parameters = {"weight1": parameters["weight1"]-learning_rate*grads["dweight1"],
                  "bias1": parameters["bias1"]-learning_rate*grads["dbias1"],
                  "weight2": parameters["weight2"]-learning_rate*grads["dweight2"],
                  "bias2": parameters["bias2"]-learning_rate*grads["dbias2"]}
    
    return parameters

Öğrenilmiş ağırlık ve bias parametreleri ile tahmin

• Vay canına yoruldum :) Buraya kadar parametrelerimizi öğreniyoruz. Verileri uydurduğumuz anlamına gelir.
• Tahmin etmek için parametrelerimiz var. Bu nedenle, tahmin edelim.
• Tahmin adımında girdi olarak x_test var ve bunu kullanırken ileriye dönük tahmin yapıyoruz.

# prediction
def predict_NN(parameters,x_test):
    # x_test is a input for forward propagation
    A2, cache = forward_propagation_NN(x_test,parameters)
    Y_prediction = np.zeros((1,x_test.shape[1]))
    # if z is bigger than 0.5, our prediction is sign one (y_head=1),
    # if z is smaller than 0.5, our prediction is sign zero (y_head=0),
    for i in range(A2.shape[1]):
        if A2[0,i]<= 0.5:
            Y_prediction[0,i] = 0
        else:
            Y_prediction[0,i] = 1

    return Y_prediction

Modelin oluşturulması

• Hepsini bir araya getirelim

# 2 - Layer neural network
def two_layer_neural_network(x_train, y_train, x_test, y_test, num_iterations):
    cost_list = []
    index_list = []
    #initialize parameters and layer sizes
    parameters = initialize_parameters_and_layer_sizes_NN(x_train, y_train)

    for i in range(0, num_iterations):
         # forward propagation
        A2, cache = forward_propagation_NN(x_train,parameters)
        # compute cost
        cost = compute_cost_NN(A2, y_train, parameters)
         # backward propagation
        grads = backward_propagation_NN(parameters, cache, x_train, y_train)
         # update parameters
        parameters = update_parameters_NN(parameters, grads)
        
        if i % 100 == 0:
            cost_list.append(cost)
            index_list.append(i)
            print ("Cost after iteration %i: %f" %(i, cost))
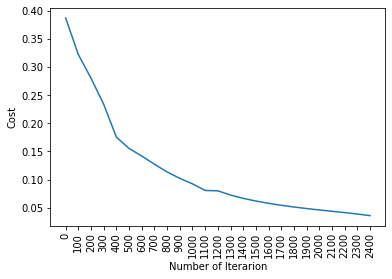
    plt.plot(index_list,cost_list)
    plt.xticks(index_list,rotation='vertical')
    plt.xlabel("Number of Iterarion")
    plt.ylabel("Cost")
    plt.show()
    
    # predict
    y_prediction_test = predict_NN(parameters,x_test)
    y_prediction_train = predict_NN(parameters,x_train)

    # Print train/test Errors
    print("train accuracy: {} %".format(100 - np.mean(np.abs(y_prediction_train - y_train)) * 100))
    print("test accuracy: {} %".format(100 - np.mean(np.abs(y_prediction_test - y_test)) * 100))
    return parameters

parameters = two_layer_neural_network(x_train, y_train, x_test, y_test, num_iterations=2500)

Cost after iteration 0: 0.386967
Cost after iteration 100: 0.321984
Cost after iteration 200: 0.279984
Cost after iteration 300: 0.233644
Cost after iteration 400: 0.175235
Cost after iteration 500: 0.155226
Cost after iteration 600: 0.141642
Cost after iteration 700: 0.127217
Cost after iteration 800: 0.113395
Cost after iteration 900: 0.102101
Cost after iteration 1000: 0.092295
Cost after iteration 1100: 0.080616
Cost after iteration 1200: 0.079875
Cost after iteration 1300: 0.072377
Cost after iteration 1400: 0.066567
Cost after iteration 1500: 0.061786
Cost after iteration 1600: 0.057735
Cost after iteration 1700: 0.054234
Cost after iteration 1800: 0.051160
Cost after iteration 1900: 0.048416
Cost after iteration 2000: 0.045918
Cost after iteration 2100: 0.043571
Cost after iteration 2200: 0.041240
Cost after iteration 2300: 0.038709
Cost after iteration 2400: 0.035777

train accuracy: 99.42528735632185 %
test accuracy: 93.54838709677419 %

• Bu noktaya kadar 2 katmanlı sinir ağı oluşturup nasıl uygulayacağımızı öğreniyoruz.
  • Katmanların boyutu ve başlatma parametreleri ağırlıkları ve bias değerleri
  • İleri yayılma
  • Loss fonksiyonu ve cost fonksiyonu
  • Gradyan İniş ile Optimizasyon Algoritması
  • Geri yayılım
  • Güncelleme Parametreleri
  • Öğrenilmiş parametreler ağırlık ve bias ile tahmin
  • Model Oluşturma

Şimdi L katmanlı sinir ağını keras ile nasıl uygulayacağımızı öğrenelim.